数字だけでなく、a,x,y などの文字も使って表していますね。 左の2つの式が表す意味はなんとなくわかりそうです。 10a ・・・ 10とaを足す x-5 ・・・ xから5を引く第1章 式の計算 <前: L8 文字式の利用 (整数の性質) の問題 L9 文字式の利用 (図形の性質) の解答 :次> 練習問題1 1辺の長さが a の正方形がある。 この正方形の1辺の長さを2倍したとき、周の長さと面積はそれぞれ何倍になるか答えなさい中学数学式による説明 位どり 例題1 \(2\) けたの整数と、その数の十の位の数と一の位の数を入れかえた数との差は、\(9\) の倍数になることを文字を使って説明しなさい。

中学2年の数学 動画 文字式の利用 カレンダー編の問題 19ch
数学 文字式による説明
数学 文字式による説明-係を調査し、文字式を意義あるものとして主 体的に学習することを促す指導法への示唆を 得ることである。 2.研究の背景 21 文字式利用の意義 数学学習において、文字式の果たしている 役割や意義は大きい。次の①~⑦は、文字式立て説明し伝え合う活動を取り入れる必要がある。その活動を通して、文字式の有用性に気付 かせたい。 文字式による説明に関する見方や考え方を伸ばしていくため,考え方や文字の使い方の共通 点や相違点に目が向くよう話し合いをさせる。




文字式による説明 後半 2桁の自然数 カレンダー 教遊者
中2「文字式による説明」の教え方 中学数学 説明がメインとなる単元は以下の2つ。 ・中2一学期の文字の利用での、倍数奇数偶数になることの説明 ・中2二学期の三角形の合同などの図形の証明 今回は前者の方を取り上げます。 説明問題は大抵どの子も苦手ですが、その理由のほとんどは単純に書き方を知らないだけです。 よって 最初は型を覚えさせる 単元 文字式の利用, 「中2の式による説明をまとめたものです。 書き方の流れをまとめているので、参考にどうぞ。」, 学年 中学2年生, キーワード 中2数学,式の説明 中学2・3年生 数学式による説明のコツ③文字が2つ必要なパターン徹底解説1学期中間テスト範囲 https//bestmannet/blog/representation47/ 「式による説明」 問題具体例と模範
*文字を使って数をどう表すかが大切になります。基本的な表しかたを確認してください。 整数,自然数は n や m の文字で表すことが多いです。 (証明がしっかり書けていればxやyなど他の文字で定義されていても正答になります。式による説明 1 nを整数とする。次の文字式はどんな数を表すか、答えよ。 ① 3n ② 2n1 2 nを整数とするとき、次の数を文字式であらわしなさい。About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
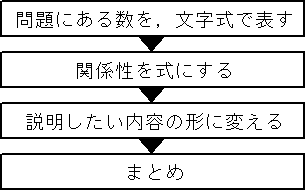
文字式の利用の問題の解き方がわかる3ステップ 文字式の利用の解き方はたったの3ステップさ。 例題をときながらみていこう! 2つの整数が、偶数と奇数のとき、その和は奇数になります。 そのわけを説明しなさい。 Step1 数字を文字式であらわすっ! 問題文の「数字」を「文字」であらわしてみよう! えっ。式による説明 解答の仕方 式による説明 式による説明は3つの部分でできている。 1つ目は 文字で表す。 2つ目は 計算。 3つ目は 結論 。 例1) 次のことがらを式によって説明する 3つの連続する偶数 の和は 6の倍数になる。関係を,文字式を用いて簡潔かつ一般的に考察す ることができる。 ・数学的な表現・処理 事象を文字式を使って表現したり,文字式が意 味することを読みとったり,一般的な説明をする ことができる。 ・数量・図形などについての知識・理解




中2数学 文字式の利用の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中2数学 式の計算 文字式の利用 式による説明が解ける たけのこ塾 勉強が苦手な中学生のやる気をのばす
3 式による説明 (本時3/3) 式を利用する ことに関心をも ち,式による説明 したりしようと している。 数量の関係 や性質につい て,文字を用 いて一般的に 説明すること ができる。 事象を文字式 で表したり,文 字式が表す具体 的場面をよみと ったり 文字式の単元を進めていく上で 最も大切な基礎部分にあたる 文字式の表し方のきまりについて 説明をしていきます。 この文字式のルールをしっかりと覚えておかないと 次には進めないからね 気合を入れて、学習していこう! 具体例を使いながら 中学数学:中2文字式を使った説明⑥宮城県入試問題 こんにちは。相城です。今回は文字式を使った説明の問題で, 宮城県の入試問題を解いてみましょう。 それではどうぞ。 を一の位が0でない2けたの自然数とし, の十の位の数字を, 一の位の数字を とし



文字と式 式による説明 の問題を解くときのポイント 中学数学 定期テスト対策サイト




中2数学 文字式による説明3 5分で学習 Youtube
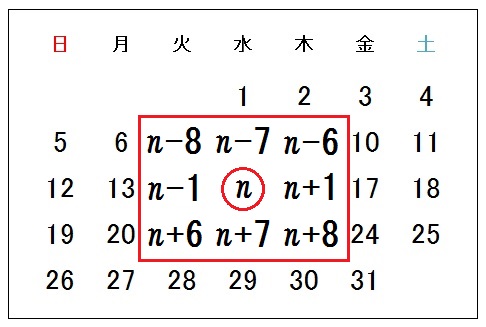
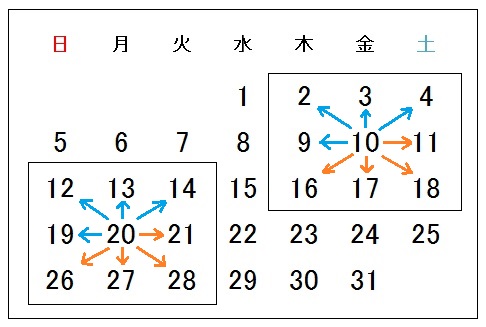
① 真ん中をY とすると前後の数はY − 7,Y + 7と表される。② (Y − 7) + Y + (Y+7)= 3 Y 3Yは3の倍数なので、わくをどこにとっても、3つの数の和は3の倍数になる ①9 = 8+1 13 = 8+ 5= 8 + 4 +1文字を使った式について学んだ ことを生活や学習に生かそうと している。 文字を使った式を活用した問題 解決の過程を振り返って検討し ようとしている。 1 式による説明 (教科書p22~24) 10 数の性質が成り立つこと を,文字を使って説明する== 文字式による説明 == 2けたの整数を表すことができるが、 ab のように2つの文字を続けて書くと、これらは「文字式 問題 次の空欄に入るものを右の選択肢から選んで、説明




中学2 3年生 数学 式による説明のコツ 例題集と模範解答例 こんな問題が出題される




中2 式の計算 文字式による説明 前半 整数 自然数 偶数 奇数 デジタル板書データ Youtube
等式の変形1 等式の変形2 等式の変形3 等式の変形 (入試問題) 等式の変形 (発展学習) → スg スム版は別包ソス ス ス ス ス スフ撰ソス ス ス ス ス ス ス ス ス ス スニゑソス ス謔ュ スg ス ス ス ス ス ス I ス@ ス ス ス スA ス n ス ス ス スR ス ス スi ス スWord による数式入力マニュアル(H 版) 愛知県高等学校数学研究会 (Unicode 文字コードのサポート) ・マウスを使わずに、キーボードのみの操作でも数式を入力できるようになった。2 年 1 21 ~24 年度用中学校数学 年間指導計画案・評価規準例第2学年 1章式の計算(14) 学習指導要領内容a(1) 章の目標 ①文字を用いた式についての基礎的な概念や原理・法則などを理解するとともに,事象を数学化したり,数学的に解釈したり,数学的に表現・処理したりする技能を身に




中学2 3年生 数学 式による説明のコツ 文字が2つ必要なパターン徹底解説 1学期中間テスト範囲




文字式による説明2ver2 中学数学 講義 Youtube
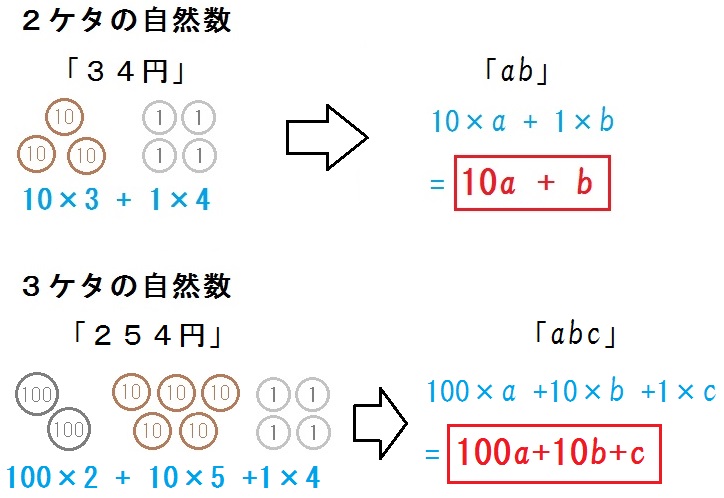
中2数学 文字式による説明② 前回の続きです。 前回は、「nを整数として3×n」これですべての3の倍数をノートに書き表せるというところまでお話ししました。 ( 前回のブログ記事はこちら ) すごいことですよね。 3,6,9,と書いていっても絶対にすべて書き表せない3の倍数を、わずか数文字で表しています。 これをふまえて例題 連続する \(3\) つの整数の和は、\(3\) の倍数になることを、文字を使って説明しなさい。 解説 初めてこの問題を見て、何がなんやらポカーンとなっているみなさん。 大丈夫です。 一からしっかりと解説をしていき文字式を利用するといろいろな事柄を説明することができます。まずは $2$ けたの自然数を文字で表してみましょう。 十の位を $\textcolor{blue}{a}$ 、一の位を $\textcolor{blue}{b}$ とすると、$2$ けたの自然数は $\textcolor{blue}{10ab}$ と表すことができます。
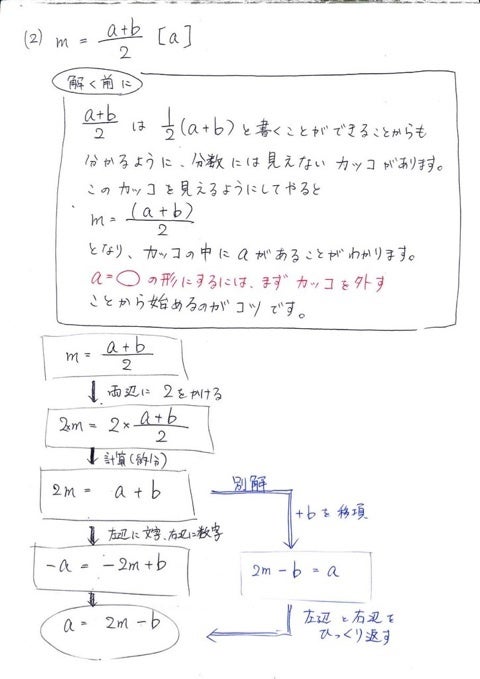



この問題解ける 中2数学 文字式の利用 等式の変形と式による説明 葉美カフェの片隅で一人おしゃべり
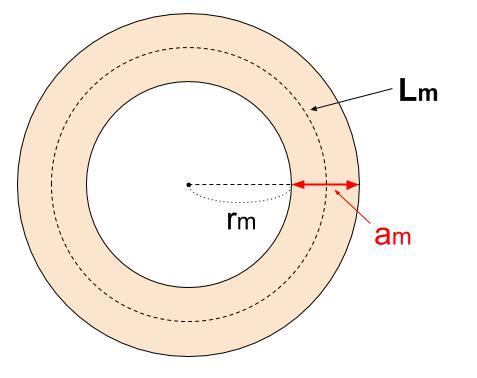



中学数学 式による説明 図形 中学数学の無料オンライン学習サイトchu Su
文字を含んだ式の、 ・足し算や引き算なら普通にできるけど ・「説明しなさい」と来ると難しく感じる という生徒さんは多いですね。 でも、そんなに難しくないので、 まずは一番大事なルールをひとつ。 数学では、 「ある数」を n と表す ことが多いNを整数とすると連続する3つの偶数は2n,2n2,2n4となる。 これらの和は2n (2n2) (2n4)=6n6 =6 (n1) nが整数なので (n1)も整数となり6 (n1)は6の倍数である。 よって連続する3つの偶数の和は6の倍数になる。 nを整数とすると4つの連続する奇数は2n1,2n3,2n5,2n7となる。 これらの和は (2n1) (2n3) (2n5) (2n7)=8n16 =8 (n2) nは整数なので (n2)も整動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
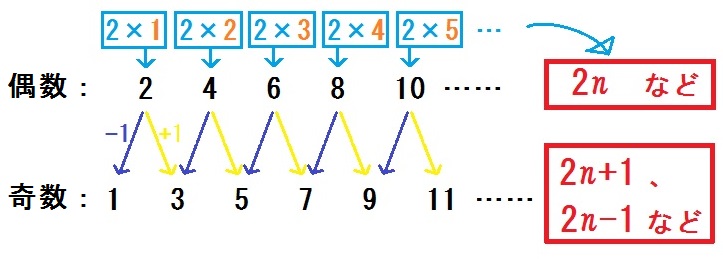



中学数学 式による説明 のコツと練習問題




ベスト中 2 数学 式 による 説明 最高のカラーリングのアイデア
文字式による説明 学習指導案 (PDF) 版 1 著者 川村 栄之 授業日 13年07月02日 学校名 東京学芸大学附属小金井中学校 指導者 川村 栄之 対象学年 中学校2年生(14 years old) 教科 算数 レーティング レーティングボタンを表示するにはFacebookのアカウントが必要です。FdData 中間期末:中学数学2 年:文字式の利用 文字式による説明:2 けた(3 けた)の整数/奇数と偶数/連続する整数/連続する奇数(偶数) /カレンダーなど/商と余り/等式の変形/文字式の図形 『式による説明』では、答えの書き方が決まっています。 書き方の「型(かた)」を最初に覚えて、どんな問題でも同じパターンにのっとって書くのが、実は一番効率的で簡単です。 まず、やさしい問題で、書き方の定型を覚えましょう。 例題1:「奇数と奇数の和は偶数である。




文字式による説明 前半 整数 偶数 奇数 教遊者




中学数学2年 文字式の利用 商と余り 受験の月
授業実践記録(数学) 全国の先生方による工夫された数学の授業実践を「授業実践記録」として紹介します。 なお,以前に紹介していました「課題学習の指導」 (1998年4月~05年3月)と「実践記録」 (1998年4月~1999年2月)もここにまとめました。 19年1月 中学2・3年生 数学式による説明のコツ②"連続する~"パターン別徹底解説1学期中間テスト範囲 next 中学2・3年生 数学式による説明のコツ④ 例題集と模範解答例こんな問題が出題される! 中2 数学 文字式による説明③ 前回は、「3の倍数と3の倍数の和が、3の倍数になることをどのように説明したらよいか? 」というところまで話が進みました。 ( 文字式による説明①はこちら ) すべての3の倍数を表せないことにははじまらない、という




数学 中2 11 文字式の利用 2けたの自然数編 Youtube




ベスト中 2 数学 式 による 説明 最高のカラーリングのアイデア
た式を使って一般的に説明することの有用性と意味を感 じた生徒が多かった。また,友だちのレポートを見て, 「同じ性質を説明しているのに,何を文字で置くかによ って計算や式の変形が変わっている」,「最後の変形のとA=132を11で割ってみると,132÷11=12となり,132は11の倍数であることが分かります。 スポンサードリンク また,A=275の場合,百の位は2,一の位は5で,これらを足すと25=7となり,十の位の数と等しくなります。 この場合も,A=275を11で割ってみると,275÷11=25となり,275は11の倍数であることが分ります。 これを,「文字を使って」証明していきましょう。




文字式による説明4 中学数学 講義 Youtube




中学数学 式による説明 のコツと練習問題




中2数学 式による説明 基礎編 Youtube




式による証明 無料で使える中学学習プリント




中学数学2年 文字式の利用 3 4 9の倍数条件 受験の月




中学数学 式による説明 のコツと練習問題




中学数学 式による説明 のコツと練習問題




式による証明 無料で使える中学学習プリント




中学2年の数学 動画 文字式の利用 カレンダー編の問題 19ch



文字式による説明 国際算数数学授業研究プロジェクト Impuls International Math Teacher Professionalization Using Lesson Study




中学数学 式による説明 のコツと練習問題



中学2年生の 文字式の利用 の問題です 問題右のカレンダー 下の写真 のよ Yahoo 知恵袋




中2数学 文字式による説明5 5分で学習 Youtube




中学数学1年 文字式の表し方 積 商 四則 受験の月



1



中学数学 式による説明 のコツと練習問題




ベスト中 2 数学 式 による 説明 最高のカラーリングのアイデア




文字式による説明 後半 2桁の自然数 カレンダー 教遊者




無料 中3数学 基本解説 解答プリント 307 式の計算7 式の計算の利用




中2 数学 文字式を使った説明 中学生 数学のノート Clear




数学 中2 10 文字式の利用 問題編 Youtube




この問題解ける 中2数学 文字式の利用 等式の変形と式による説明 葉美カフェの片隅で一人おしゃべり



1



Http Www Fdtext Com Dat Suub2 1siki 3ouyou Pdf




無料 中2数学 基本問題 問題プリント 5 式の計算5 文字式の利用




式の計算 式による図形の証明問題の解き方のコツ 中学数学 定期テスト対策サイト



U9j580gf8iba369ji2w Xyz P 2



中学数学 式による説明 のコツと練習問題




Akiya Su No Twitter 中学数学 文字式の利用 文字を使ってさまざまな数字を表す 多くなったので 文字式を利用した説明は明日 少し見にくいね 中学数学 文字と式 文字式の利用 整数




中1数学 文字式とは何か そして表し方のルールは5つです ひっそりと物理や数学を解説する




Akiya Su 中学数学 文字式の利用 標準レベルでは問題文のバリエーションは少ないので ワークなどでやりこむと良いでしょう 中学数学 文字と式 文字式の利用 整数




中2数学 式による説明 21 24 赤城 ᐡᐤᐡ




Akiya Su No Twitter 中学数学 文字式の利用 文字を使ってさまざまな数字を表す 多くなったので 文字式を利用した説明は明日 少し見にくいね 中学数学 文字と式 文字式の利用 整数



数学文字式の利用 連続する5つの整数の和は5の倍数であることを 文字式を使 Yahoo 知恵袋




中2 中2数学 式による説明のポイント 中学生 数学のノート Clear




高校入試数学 文字式による説明 19年度 北海道 Youtube




中2数学 式の計算 文字式の利用 式による説明が解ける たけのこ塾 勉強が苦手な中学生のやる気をのばす



Www Moka Tcg Ed Jp Nakajhsc Wysiwyg File Download 1 4939




中2 数学 式による説明 等式の変形 中学生 数学のノート Clear




文字式による説明




式による説明の問題の解き方 連続する自然数 1 現役塾講師のわかりやすい中学数学の解き方




中2数学 式の計算 文字式の利用 式による説明が解ける たけのこ塾 勉強が苦手な中学生のやる気をのばす




中1 文字と式 文字式の利用 数字と文字を行ったり来たりしながら 教えたい 人のための 数学講座




中2 数学 文字式による説明 富士宮教材開発 井出進学塾




中学2年生 数学 文字式の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




式による説明 3 知らないと解けない難問2題 Shun Ei Note




式による説明 現役塾講師のわかりやすい中学数学の解き方




文字式の利用 中学二年生 クラス授業 海星学院 泉校 京都府八幡市男山泉3 21




文字式による説明 後半 2桁の自然数 カレンダー 教遊者



1



中2 文字式による説明 の教え方 塾講師 数学マンは踊る




無料 中2数学 基本解説 問題プリント 5 式の計算5 文字式の利用




中2数学 文字式による説明 富士宮教材開発 井出進学塾




文字式 数量の表し方 関係を表す式 単位の変換問題などを解説 数スタ




元の中2 数学 文字式の利用 カレンダー 最高のカラーリングのアイデア




中2 中2数学 文字式の利用 中学生 数学のノート Clear




中2 数学 文字式による説明 富士宮教材開発 井出進学塾




中2数学 文字式の利用の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




文字式による説明 前半 整数 偶数 奇数 教遊者




平成25年長野県立高校 入試問題 式による説明の問題 現役塾講師のわかりやすい中学数学の解き方




中2 中2数学 式による説明のポイント 中学生 数学のノート Clear




文字式による説明 後半 2桁の自然数 カレンダー 教遊者




式による説明 10 カレンダーの問題 大阪のプロ家庭教師が できない を できる に変える




数学の式による説明のところって 書く形式みたいなのが決まってるんですか Clear
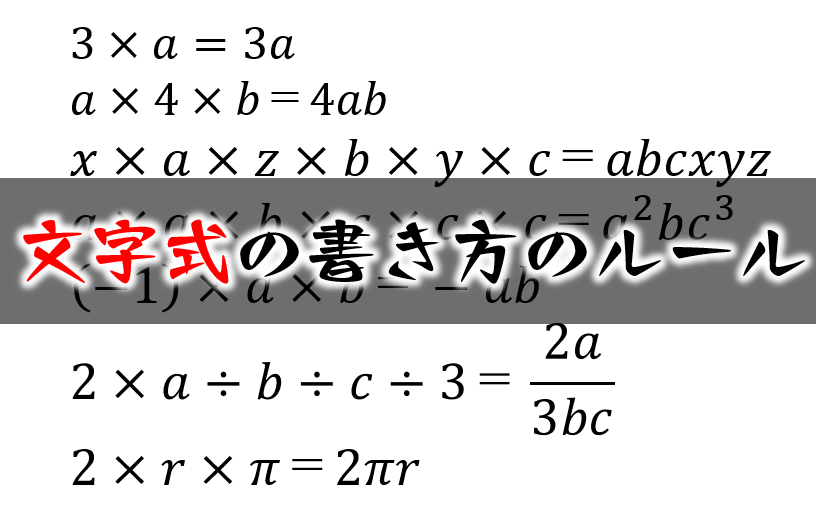



文字式の書き方のルール 数学fun




中3数学 文字式による説明 基本事項 Youtube




大分県入試問題解説 4 中2数学 文字を使った式による説明 Youtube



中学数学 式による説明 のコツと練習問題




中2数学 文字式の利用の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学 式による説明 のコツと練習問題




式による説明 現役塾講師のわかりやすい中学数学の解き方




中学数学 式による説明 のコツと練習問題



楽天ブックス 自由自在中学数学 平成28年改訂 基礎から入試まで 河野芳文 本




中2数学 式の計算 文字式の利用 式による説明が解ける たけのこ塾 勉強が苦手な中学生のやる気をのばす




数学2年 文字式の利用 塾の先生が作った本当に欲しいプリント 楽天ブログ




中学数学 中2文字式を使った説明 宮城県入試問題 数樂管理人のブログ
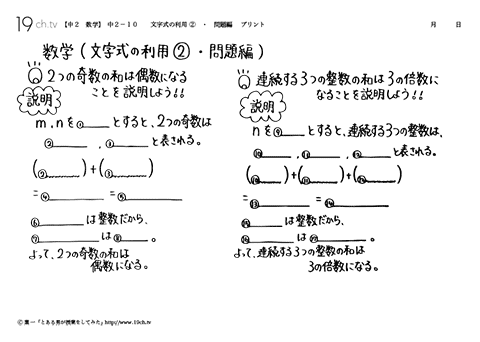



中学2年の数学 動画 文字式の利用 問題編の問題 19ch




中学数学 式による説明 図形 中学数学の無料オンライン学習サイトchu Su



2



1




中2数学 文字式による説明 5分で学習 Youtube




式による証明 無料で使える中学学習プリント




中3数学 式による説明 整数の証明のポイントと練習問題
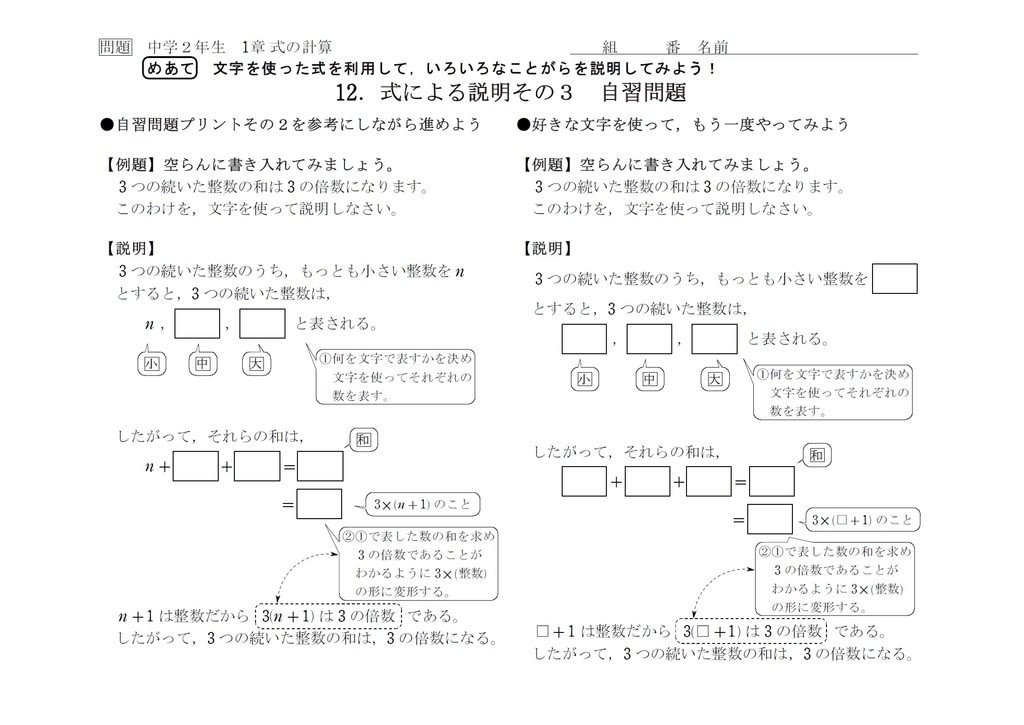



中2自習 式の計算 特別版 3 中学数学の勉強に



2




式の説明のカレンダーl字型説明の仕方を教えてください Clear




中2数学 式による説明 21 24 赤城 ᐡᐤᐡ




数学 中2 9 文字式の利用 基本編 Youtube



0 件のコメント:
コメントを投稿